HAEMOPHILUS Example of sequence statistics and gene finding with MATLAB
This demonstration looks at some statistics about the DNA content of the Haemophilus Influenzae. It shows also some algorithms for finding ORFs and for assessing their significance.
Contents
Introduction
Haemophilus influenzae is a non-motile Gram-negative coccobacillus first described in 1892 by Dr. Robert Pfeiffer during an influenza pandemic. It is generally aerobic, but can grow as a facultative anaerobe. It is responsible for a wide range of clinical diseases. The Haemophilus influenzae genome was the first to be sequenced and assembled in a free-living organism. It contains about 1.8 million base pairs and is estimated to have 1,740 genes.
Accessing NCBI data from the MATLAB workspace
The dna sequence can be obtained from the GenBank database with the accession number NC_000907. Using the getgenbank function with the ‘SequenceOnly’ flag just the nucleotide sequence is loaded into the MATLAB workspace.
Hflu = getgenbank('NC_000907','SequenceOnly',true);
If you don’t have a live web connection, you can load the data from a MAT-file using the command
% load Hflu % <== Uncomment this if no internet connection
The MATLAB whos command gives information about the size of the sequence.
whos Hflu
Name Size Bytes Class Hflu 1x1830138 3660276 char array Grand total is 1830138 elements using 3660276 bytes
The total length of the Haemophilus Influenzae genome is 1830138 bp.
Statistical sequence analysis
You will examine some statistics properties of the sequence. You can look at the composition of the nucleotides with the basecount function.
bases=basecount(Hflu)
Warning: Ambiguous symbols 'NKRNNRNSSNYKMMRSYNNNNYKNNNNSYWNMMMNKWNWYNNNSMRNNWNNWMKKNMYKNNKNYWRNKKSWNNNSSNNNNWYWSNNNYKNNRNRSSRMKRKMSKMNNWNWNYRYN' appear in the sequence. These will be in Others.
bases =
A: 567623
C: 350723
G: 347436
T: 564241
Others: 115
The four nucleotides are not used at equal frequency across the genome: A and T are much common than G and C.
Others symbols occur in the sequence. They correspond to positions in the sequence that are are not clearly one base or another and they are due, for example, to sequencing uncertainties. In this case for example: N: aNy base –
K: G or T –
R: A or G (puRine) –
Y: C or T (pYrimidine) –
M: A or C (aMino) –
S: C or G –
W: A or T.
Instead of grouping other simbols together, you can count them individually.
bases=basecount(Hflu,'Others','Full')
bases =
A: 567623
C: 350723
G: 347436
T: 564241
R: 10
Y: 11
K: 14
M: 11
S: 12
W: 11
B: 0
D: 0
H: 0
V: 0
N: 46
Gap: 0
You can also calculate the frequency of each nucleotide.
[bases frequency]=basecountfrequency(Hflu,'Others','Full')
bases =
A: 567623
C: 350723
G: 347436
T: 564241
R: 10
Y: 11
K: 14
M: 11
S: 12
W: 11
B: 0
D: 0
H: 0
V: 0
N: 46
Gap: 0
frequency =
A: 0.3102
C: 0.1916
G: 0.1898
T: 0.3083
R: 5.4641e-06
Y: 6.0105e-06
K: 7.6497e-06
M: 6.0105e-06
S: 6.5569e-06
W: 6.0105e-06
B: 0
D: 0
H: 0
V: 0
N: 2.5135e-05
Gap: 0
It should be pointed out that these are on the 5′-3′ strand of DNA, but we know exactly the frequency of all the the bases on the other strand because of the complementarity of the double helix. Anyway we could verify it using again the basecountfrequency function.
[bases frequency]=basecountfrequency(seqrcomplement(Hflu),'Others','Full')
bases =
A: 564241
C: 347436
G: 350723
T: 567623
R: 11
Y: 10
K: 11
M: 14
S: 12
W: 11
B: 0
D: 0
H: 0
V: 0
N: 46
Gap: 0
frequency =
A: 0.3083
C: 0.1898
G: 0.1916
T: 0.3102
R: 6.0105e-06
Y: 5.4641e-06
K: 6.0105e-06
M: 7.6497e-06
S: 6.5569e-06
W: 6.0105e-06
B: 0
D: 0
H: 0
V: 0
N: 2.5135e-05
Gap: 0
CG content
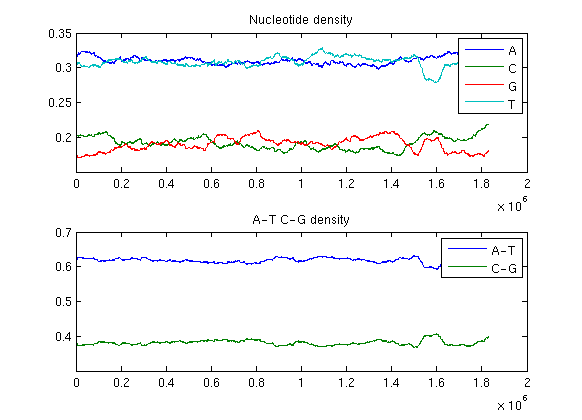
The local fluctuations in the frequencies of nucleotides provide different interesting information. The local base composition by a sliding window of variable size can be measured. In the following the window size is assumed 90000 bp and 20000 bp respectively.
ntdensity1(Hflu,'window',90000)
ntdensity1(Hflu,'window',20000)
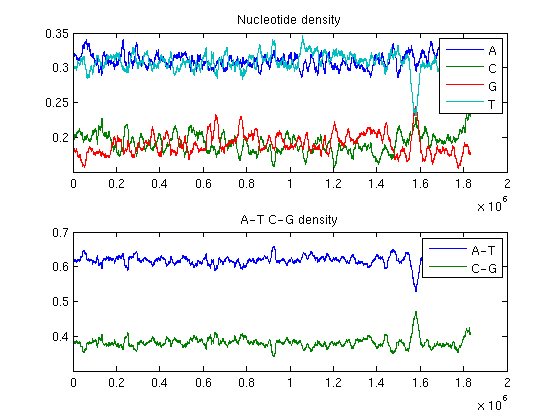
The phenomenon called horizontal gene transfer can be observed in the second plot: the H. influenzae genome contains a 30Kb region of unusual GC content from 1.56Mb to 1.59Mb.
k-mer frequency and motif bias
Now look at the dimers in the sequence and display the 2-mer frequencies in the table matrix. The simbols others than A, C, G, T are not considered.
[dimers,matrix] = dimercount(Hflu)
Warning: Ambiguous symbols 'NKRNNRNSSNYKMMRSYNNNNYKNNNNSYWNMMMNKWNWYNNNSMRNNWNNWMKKNMYKNNKNYWRNKKSWNNNSSNNNNWYWSNNNYKNNRNRSSRMKRKMSKMNNWNWNYRYN' appear in the sequence. These will be in Others.
dimers =
AA: 219880
AC: 92410
AG: 88457
AT: 166837
CA: 121618
CC: 68014
CG: 72523
CT: 88551
GA: 94125
GC: 95529
GG: 66448
GT: 91314
TA: 131955
TC: 94745
TG: 119996
TT: 217512
Others: 223
matrix =
0.1202 0.0505 0.0483 0.0912
0.0665 0.0372 0.0396 0.0484
0.0514 0.0522 0.0363 0.0499
0.0721 0.0518 0.0656 0.1189
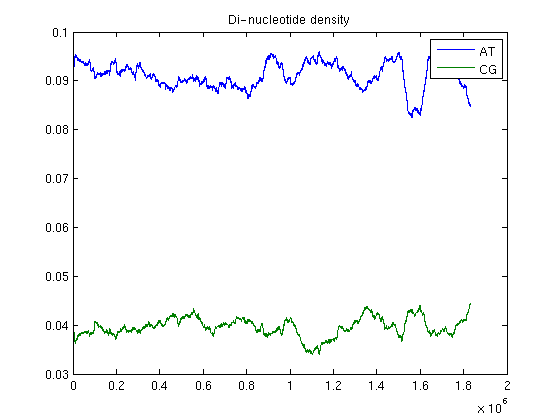
You can also plot the frequency of certain di-nucleotides of interest: for example considering the local fluctuations in the frequencies of dimers AT and CG.
density = dndensity(Hflu)
As a further analysis you can also compare the observed frequency of each dimer with the one expected under the multinomial model. This is called genome signature.
gs=gensign(Hflu)
Warning: Ambiguous symbols 'NKRNNRNSSNYKMMRSYNNNNYKNNNNSYWNMMMNKWNWYNNNSMRNNWNNWMKKNMYKNNKNYWRNKKSWNNNSSNNNNWYWSNNNYKNNRNRSSRMKRKMSKMNNWNWNYRYN' appear in the sequence. These will be in Others.
Warning: Ambiguous symbols 'NKRNNRNSSNYKMMRSYNNNNYKNNNNSYWNMMMNKWNWYNNNSMRNNWNNWMKKNMYKNNKNYWRNKKSWNNNSSNNNNWYWSNNNYKNNRNRSSRMKRKMSKMNNWNWNYRYN' appear in the sequence. These will be in Others.
gs =
1.2491 0.8496 0.8210 0.9535
1.1182 1.0121 1.0894 0.8190
0.8736 1.4349 1.0076 0.8526
0.7541 0.8763 1.1204 1.2505
You can look at codons using codoncount. That function counts the codons on a particular reading frame. With no options, the function shows the codon counts on the first reading frame.
codoncount(Hflu)
Warning: Ambiguous symbols 'NKRNNRNSSNYKMMRSYNNNNYKNNNNSYWNMMMNKWNWYNNNSMRNNWNNWMKKNMYKNNKNYWRNKKSWNNNSSNNNNWYWSNNNYKNNRNRSSRMKRKMSKMNNWNWNYRYN' appear in the sequence. These will be in Others. AAA - 27760 AAC - 11523 AAG - 11701 AAT - 22178 ACA - 9121 ACC - 7249 ACG - 6917 ACT - 7801 AGA - 8763 AGC - 8142 AGG - 5340 AGT - 7569 ATA - 12768 ATC - 11041 ATG - 10029 ATT - 22007 CAA - 15527 CAC - 7692 CAG - 6634 CAT - 10049 CCA - 9185 CCC - 3866 CCG - 4213 CCT - 5502 CGA - 6311 CGC - 6771 CGG - 4112 CGT - 7255 CTA - 6110 CTC - 4112 CTG - 6625 CTT - 11985 GAA - 12946 GAC - 3624 GAG - 4202 GAT - 10719 GCA - 10832 GCC - 6310 GCG - 6537 GCT - 8153 GGA - 5296 GGC - 6218 GGG - 3590 GGT - 7147 GTA - 7714 GTC - 3651 GTG - 7741 GTT - 11118 TAA - 16924 TAC - 7723 TAG - 6372 TAT - 12561 TCA - 11592 TCC - 5542 TCG - 6240 TCT - 8663 TGA - 11513 TGC - 10991 TGG - 9045 TGT - 9079 TTA - 17139 TTC - 12550 TTG - 15162 TTT - 27184 Others - 110
Exploring the Open Reading Frames (ORFs)
In a nucleotide sequence an obvious thing to look for is if there are any open reading frames. The function seqorfs can be used to determine the ORFs in a sequence.
orf=seqorfs(Hflu);
The variable orf is a structure with information about the start/stop positions of each ORFs, its length and which reading frame it is in. Here the minimun number of codons for an ORF to be considered valid is 10 (default value).
The minimun number of codons for an ORF to be considered valid can be also set. Here a threshold of 70 and 80 amino acids are considered leading to about 2175 and 1966 ORFs respectively.
[orf n_70]=seqorfs(Hflu,'MINIMUMLENGTH',70);
n_70
n_70 =
2175
[orf n_80]=seqorfs(Hflu,'MINIMUMLENGTH',80);
n_80
n_80 =
1966
You can also look for the total number of ORFs
[orf n]=seqorfs(Hflu,'MINIMUMLENGTH',1);
n
n =
37500
Detecting significant ORFs
The classic approach to decide whether an ORF is a good candidate as a gene is to calculate the probability of seeing an ORF of a certain length L in a random sequence. To test the significance of ORFs a single-nucleotide permutation test can be used.
[orf1 n1]=seqorfs(Hflu(randperm(length(Hflu))),'MINIMUMLENGTH',1);
n1
n1 =
52174
The ORF Length of the original and of the randomized sequences can be compared.
ORFLength=[]; for i=1:6 ORFLength=[ORFLength; orf(i).Length']; end ORFLength1=[]; for i=1:6 ORFLength1=[ORFLength1; orf1(i).Length']; end
A threshold must be chosen in order to keep as candidate genes those ORFs in the H. Influenzae genome that are longer than most (or all) the ORFs in the random sequence.
max_threshold=max(ORFLength1) n_max=length(find(ORFLength>=max_threshold))
max_threshold =
573
n_max =
1182
You can also use a more tolerant threshold in order to keep all ORFs of length equal to or greater than the top 1% of random ORFs.
empirical_threshold=prctile(ORFLength1,99) n_emp=length(find(ORFLength>=empirical_threshold))
empirical_threshold =
207
n_emp =
2209